---

本連載を書籍化した、「基礎からの材料力学 (JSMEやさしいテキストシリーズ) 」が発行されました。機械工学への新たな一歩を踏み出す学生の方々、学びなおしの一冊として教科書をお探しの社会人の方々にふさわしい新定番の教科書です。　Kindle版　／　単行本（ソフトカバー）版　

YouTubeで「JSMEやさしいテキストシリーズ”材料力学”」の紹介動画が視聴できます！

第1回：応力とひずみ (17:12)

---

＜本連載にあたって＞

機械工学に携わる技術者にとって，「材料力学，機械力学，熱力学，流体力学」の4力学は，欠くことのできない重要な学問分野である。しかしながら昨今は高等教育でカバーすべき学問領域が多様化しており，大学や高等専門学校において，これら基礎力学の講義に割かれる講義時間が減少している。本会の材料力学部門では，主に企業の技術者や研究者を対象として材料力学の基礎を学ぶための講習会を毎年実施しているが，そのなかで，企業に入ってから改めて材料力学の基礎の基礎を学びなおすための教科書や参考書がぜひ欲しいという声があった。また，電気系や材料科学系の技術者からも，初学者が学べる読みやすいテキストを望む意見があった。これらのご意見に応えるべく，本会では上記の4力学に制御工学を加えた5分野について，「やさしいシリーズ」と題する教科書の出版を計画している。今回は本シリーズ出版のための下準備も兼ねながら，材料力学の最も基礎的な事項に絞って，12回にわたる連載のなかで分かりやすく解説させて頂くことにしたい。

1　はじめに

本稿では，材料力学を学ぶにあたってもっとも大切な応力とひずみの概念について学ぶ。ひずみと応力の定義，応力とひずみの関係を表すフックの法則，垂直ひずみとせん断ひずみの違いについても説明する。

2　垂直応力

図1.1に示すように，丸棒の両端に大きさが$P[{\rm N}]$の引張荷重が作用している場合について考えよう。棒の断面積を$A[{\rm m}^2]$，棒の端面作用する圧力を$\sigma[{\rm Pa}={\rm N}/{\rm m}^2]$とすると，荷重と圧力の間には

\[\sigma = \frac{P}{A}\]

(1)

の関係が成り立つ。応力$\sigma$は，${\rm Pa}={\rm N}/{\rm m}^2$の次元を持っており，物理学でいうところの圧力と同じものと考えて差し支えないが，材料力学では材料の内部に働く単位面積あたりの力のことを応力と定義し，物体の面に対して垂直方向に作用する応力のことを垂直応力と呼ぶ。垂直応力の符号は，図1.2に示すように，応力の作用する面に対してその法線と同じ向きに作用する応力，すなわち面を引張る方向に作用する垂直応力を正と定義する。一方，注目面に対して押し付ける向きに作用する圧縮応力は負の応力と定義する。

図1.1　棒に作用する引張荷重と垂直応力

図1.2　垂直応力の正負の定義

3　垂直ひずみ

ばねに荷重が作用する場合の変形を扱う際には，荷重に対して得られる変形量＝変位を考えて議論が行われる。それに対して材料力学では，材料（構造物）が絶対量としてどのぐらい変形したかということよりも，変形の割合がむしろ重要となる。これは物体の変形の割合によって，その内部に生じる応力が決定されるためである。

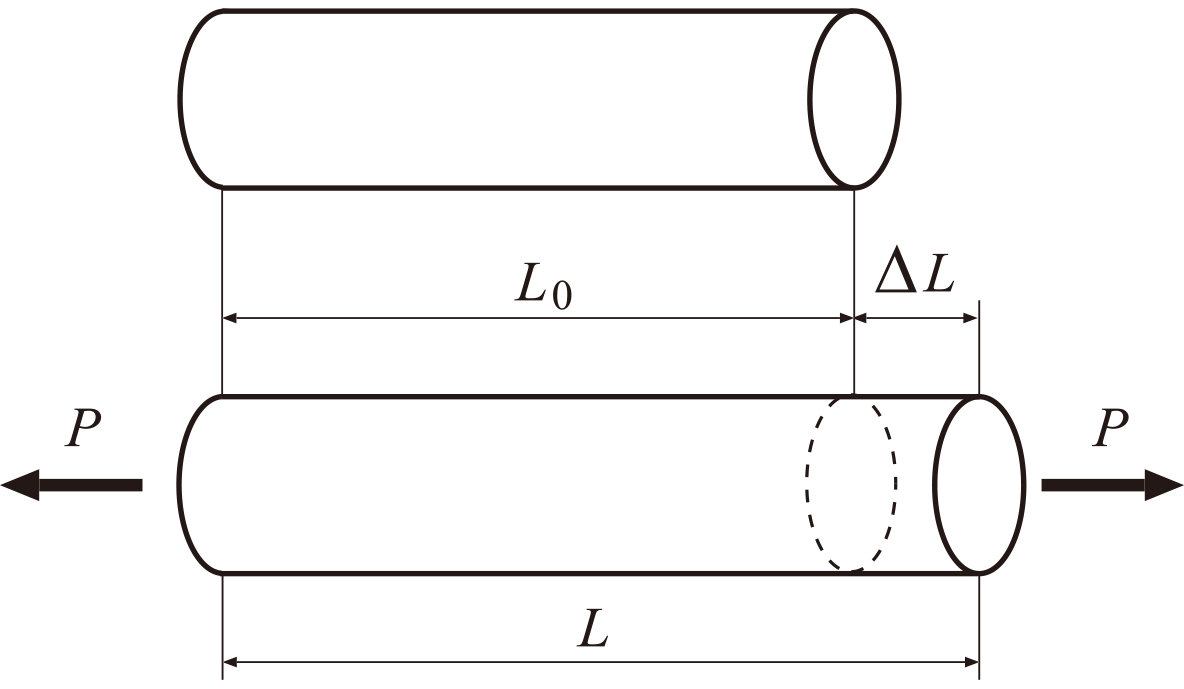
図1.3　棒の伸びとひずみ

図1.3のように，長さが$L_0$に荷重が加えられて長さが$L$になった状態を考える。棒の伸びは，

\[\Delta L = L – L_0\]

(2)

である。変形の割合を求めるために，上式の伸びを棒の元の長さ$L_0$で割って無次元化することにより得られるひずみ（垂直ひずみ）を定義する。

\[\text{垂直ひずみ：} \varepsilon = \frac{\Delta L}{L_0} = \frac{L – L_0}{L_0}\]

(3)

このひずみは物体の伸びや縮みの割合を表すもので，垂直応力に対するものとして垂直ひずみと呼ばれる。垂直ひずみは，物体（棒）が伸びた場合に正の値をとり，縮んだ場合には負の値をとることに注意したい。

ここで，物体に作用する応力と，その結果として生じるひずみは比例するものと仮定する。なお，ここでは応力とひずみの関係が比例するような，変形が十分に小さい領域に限って議論することとする。次式で定義される応力とひずみの関係式を，材料力学では一般化されたフックの法則と呼ぶ。

\[\sigma = E \varepsilon\]

(4)

ここで，$E$はヤング率ないしは縦弾性係数と呼ばれる定数であり，物体の材質のみによって決まる物性値である。なお，ひずみは無次元量であるから，ヤング率の単位は応力と同じ${\rm Pa}={\rm N}/{\rm m}^2$である。

一般的な工業材料のヤング率を記しておくと，鉄鋼材料（軟鋼）の場合，ヤング率は200～210GPa，エポキシやポリカーボネートなどの樹脂材料では2～5GPa程度の値となる。

4　ポアソン比

棒や板が引張応力を受ける場合には，その直交する方向に対して応力が作用していなくてもひずみが生じる。例えば丸棒を長手方向に引っ張って伸ばすと，棒の直径は細くなる。これを一般にポアソン効果と呼び，ポアソン効果を表す係数をポアソン比と呼ぶ。

図1.4　ポアソン比の定義

長さが$L_0$，直径が$d_0$の丸棒に引張荷重を作用させる場合について考える（図1.4）。ある荷重を受けて，この棒の長さが$L$，直径が$d$になったとすれば，この棒の長手方向（荷重方向）のひずみ$\varepsilon_x$は

\[\varepsilon_x = \frac{L – L_0}{L_0}\]

(5)

直径方向のひずみ$\varepsilon_y$は

\[\varepsilon_y = \frac{d – d_0}{d_0}\]

(6)

となる。ここで，荷重方向に対するひずみ$\varepsilon_x$と，それに直交する方向のひずみ$\varepsilon_y$の比を考えて以下の定数$\nu$を定義する。

\[\text{ポアソン比：} \nu = – \frac{\varepsilon_y}{\varepsilon_x}\]

(7)

材料力学ではこの定数$\nu$をポアソン比と呼ぶ。引張方向のひずみが正ならば，それと直交する方向のひずみは一般的に負になるので，ポアソン比の定義式にはマイナスが付くことに注意したい。均質等方性材料では，ポアソン比は0.5を超えることはなく，ほとんどの材料で0.2から0.4程度の値をとる。

5　せん断応力とせん断ひずみ

次に，図1.5に示すように，着目する面に平行な方向に作用する力であるせん断力について考える。この力を単位面積あたりの力として表したものがせん断応力となる。着目面の断面積を$A$とすれば，せん断応力$\tau$は以下のように定義される。

\[\text{せん断応力：}\tau = { Q \over A}\]

(8)

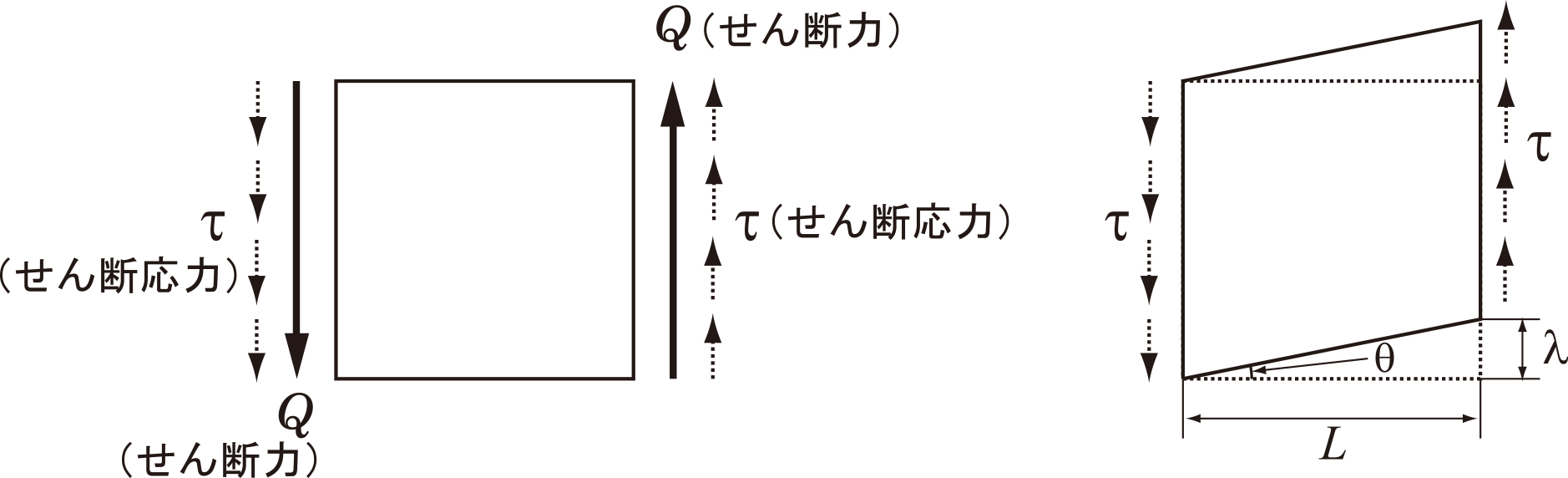
図1.5　せん断応力，せん断ひずみの定義

ここで，基準長さに対する変形量の比を考えてせん断変形を表すことを考える。いま，着目している正方形の領域の一辺の長さを$L$として，図1.5（右）に示されるように着目面と平行な方向への移動量を$\lambda$とすると，$L$と$\lambda$の比がせん断ひずみ$\gamma$となる。

\[\text{せん断ひずみ：} \gamma = \frac{\lambda}{L}\]

(9)

もし，せん断変形量$\lambda$が小さいとすれば，これらの長さと角度$\theta$の間に，$\tan \theta \simeq \theta = \lambda/L$の関係が成立するから，せん断ひずみは着目領域のせん断変形量を角度で表したものととらえることができる。

また，垂直応力と垂直ひずみの関係と同様に，せん断応力$\tau$とせん断ひずみ$\gamma$の間にも，以下のフックの法則が成立する。

\[\tau = G \gamma\]

(10)

ここで，比例定数$G$のことをせん断弾性係数（横弾性係数）と呼ぶ。材料の弾性的性質に方向性がない場合，すなわち材料が等方性材料であれば，ヤング率$E$とせん断弾性係数$G$，ポアソン比$\nu$の間に以下の関係式が成り立つ。

\[G = \frac{E}{2(1 + \nu)}\]

(11)

例えば，ヤング率206GPa，ポアソン比0.3の鉄鋼材料の場合，せん断弾性係数は79.2GPaとなる。

演習問題1.1：棒の引張

直径が10mm，長さが200mmの丸棒があり，両端に5kNの引張荷重が作用している場合について考える。この棒のヤング率を210GPaとして，棒に生じる垂直応力，棒に生じる垂直ひずみ，棒全体の伸びを求めなさい。なお，棒内部の応力とひずみは一様であるものとする。

（答：応力＝63.7MPa，ひずみ＝303$\boldsymbol{\mu}$，伸び＝60.6$\boldsymbol{\mu}{\bf m}$）

---

＜フェロー＞

荒井 政大

◎名古屋大学 工学研究科航空宇宙工学専攻 教授

◎専門：材料力学，固体力学，複合材料。有限要素法や境界要素法による数値シミュレーションなど。

---

＜正誤表＞

冊子版本記事（日本機械学会誌2019年1月号（Vol.122, No.1202））P.37におきまして、下記の誤りがありました。謹んでお詫び申し上げます。

訂正箇所	正	誤
式(7)	\[\text{ポアソン比：} \nu = – \frac{\varepsilon_y}{\varepsilon_x}\]	\[\text{ポアソン比：} \nu = – \frac{\varepsilon_x}{\varepsilon_y}\]
演習問題2行目	5kNの引張荷重	500Nの引張荷重