3.1 面に働く静止流体力

図3-1のように水中に垂直に設置された板に働く，静水圧による力を考える（静止した水中のゲージ圧を静水圧と呼ぶ）．この板の左面は水，右面は大気にそれぞれ接しており，板は水に押されて右向きの力を受けている．ここで，水面から板の重心$\mathrm{G}$までの深さを$H$，板の面積を$A$とすると，板の重心位置におけるゲージ圧は$\rho gH$となる．この板に働く力の大きさ $F$ は，$F\mathrm{=}\rho gH\cdot A$ と表され，水中に垂直に設置された板に働く力は，（板の重心地点の圧力）$\mathrm{\times }$（板の面積）で求まる．これを板の微小要素にかかる静水圧による力を積分して示そう．

図3-1 水中の面に働く静止流体力：(a) 板を側面から見た図，(b) 板の正面図

図3-1に示す板は幅 $b$ である面積が $A$ の長方形である．水面を原点として深さ方向に $z$ 座標をとり，板の上端位置を $z_1$，下端位置を $z_2$ とする．板面上深さ $z$ の位置にある，幅 $dz$ の微小要素を考えると，この微小要素に働く静水圧による力 $dF$ は，$dF\mathrm{=}\rho gz\cdot bdz$ となる．ここで，$\rho gz$ は深さ $z$ におけるゲージ圧，$bdz$ は微小要素の面積である．板全体に働く力の大きさ $F$ は，$dF$ を板全体で積分すれば得られるので，

\[F=\int^{z_2}_{z_1}{\rho gzbdz}\]

となる．ここで重心位置 $H$ は重力が代表して作用する点であるから（重心の定義），

\[\int^{z_2}_{z_1}{zbdz}=HA\]

となることを用いると $F=\rho gHA$ となる．深さ $z$ におけるゲージ圧が $\rho gz$ であったことから，板の重心地点におけるゲージ圧は $\rho gH$ である．したがって，水中に垂直に設置された板に働く力の大きさは（板の重心地点のゲージ圧）$\mathrm{\times }$（板の面積）で求まることが示された．

ここまでで板に働く静水圧による力の大きさが求まったが，一方でこの力が代表して働く位置はどこになるだろうか．平面上の静水圧による力が代表して作用する点を圧力中心と呼ぶ．水圧は水深が深いほど大きくなるので，圧力中心位置Cは重心位置とは一致しない．圧力中心位置に作用する力 $F$ によるモーメントが，板に働く全モーメントに等しくなることを利用して圧力中心位置を求めよう．図3-1に示すように圧力中心位置の水深を $\zeta $ とすると，圧力中心に作用する $F$ によるモーメント $M$ は，$M=F\zeta =\rho gHA\zeta$ となる．一方で，幅 $dz$ の微小要素に作用するモーメント${dM}^\prime$は，水面から微小要素までの距離 $z$ を用いて${dM}^\prime=z\cdot dF = z\cdot\rho gz\cdot b dz$となる．よってモーメントの総和は板全体で積分して得られ，

$${M}^\prime=\int^{z_2}_{z_1}{z\cdot \rho gz\cdot bdz}$$

となる．圧力中心位置$\zeta$は，$M={M}^\prime$が満たされる点なので，

$$\rho gHA\zeta =\int^{z_2}_{z_1}{z\cdot \rho gz\cdot bdz} \nonumber \\ \zeta =\frac{1}{HA}\int^{z_2}_{z_1}{z^2~b~dz}$$

（3.1）

と表され，この式を用いれば圧力中心位置 $\zeta $ が求まる．

上式の $\int^{z_2}_{z_1}{z^2~b~dz}$ は，水面上を原点として紙面奥行方向に定義される $x$ 軸周りの板の断面2次モーメントに等しい．これを用いれば様々な形状の圧力中心を簡単に求めることができる．一般的に断面2次モーメントは重心を原点とした軸周りに定義されることが多い．原点が重心から離れている場合の断面2次モーメントを求める際には平行軸の定理を用いる．

3.2 浮力と浮揚体の安定性

静止流体中にある物体には浮力が働き，浮力の大きさは物体が押しのけた流体にかかる重力の大きさに等しい．これはアルキメデスの原理として知られている．これを示すために，図3-2に示すような静止流体中の仮想的な角柱(角柱の上下の面の面積を $A$，角柱の高さを $h$とする)に働く力の釣り合いを考えよう．この仮想的な角柱は水中で静止しているので，この角柱にかかる静水圧による力 $F$ と重力 $W$ はつり合っている．静水圧による力は，角柱の上面を下方に押す力と，角柱の下面を上方に押す力の差となる．上面と下面の圧力差を $\mathit{\Delta}p$ とすると，$F=\mathit{\Delta}p\cdot A=\rho ghA$ となる．一方で，仮想的な角柱にかかる重力 $W$ は角柱内の流体の質量が $\rho Ah$ であることから，$W\mathrm{=}\rho Ah\mathrm{\cdot }g$ となる．これが「物体が押しのけた流体にかかる重力」である．したがって
力 $F$ は物体が押しのけた流体にかかる重力 $W$ と等しく $\rho ghA$ であり，アルキメデスの原理が説明された．仮想的な角柱が別の物体に置き換わったとしても静水圧力による力は変わらず，浮力の大きさは物体が押しのけた流体にかかる重力の大きさとして求めることができる．浮力の作用点は押しのけた流体体積の重心に一致し，浮力の作用点を浮心と呼ぶ．

図3-2 水中の面に働く静止流体力

静止流体中に浮かぶ物体（浮揚体）には，重力 $W$ と浮力 $B$ が作用している．重力と浮力それぞれの大きさ，それぞれの作用点の位置関係によって，浮揚体が安定した姿勢で浮いていられるかが決まる．図3-3に示すような幅 $b$，底面から水面までの距離 $\ell $ の奥行方向に十分長い浮揚体を考える．このとき，浮揚体が微小角度傾いた際の重心周りのモーメントのつり合いを考えることで浮揚体の安定性を確かめることができる．物体の重心 $\mathrm{G}$（図中$\mathrm{\bigstar}$表示）と浮心 $\mathrm{C}$（図中 ● 表示）が，図3-3の左側に示すような位置関係であれば，微小角度傾いた際に働く浮力による重心周りのモーメントは傾いた姿勢を元に戻す方向に作用するため姿勢は安定である．一方で，図3-3の右側に示すような位置関係になると先ほどと逆の関係となり，条件によっては姿勢が不安定となる可能性がある．このとき，図3-3右側に示すような状況では，重力と浮力の作用点の距離を$ a$ とすると $a<\frac{b^2}{12\ell }$ の条件で安定となる．$b$ を大きくする（幅を広げる），もしくは $a$ を小さくする（重心を下げる）ことで，浮揚体はより安定となる．

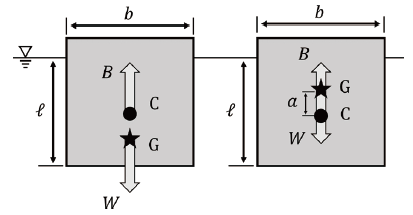
図3-3 浮揚体に働く重力と浮力の位置関係：(左)重心が浮心より下にある場合, (右)重心が浮心より上にある場合

演習問題3-1　水中に置かれた板の圧力中心位置

図3-1に示すように静止した水中に置かれた板の圧力中心位置について考える．いま$z_{\mathrm{1}}=1 \mathrm{m}, z_{\mathrm{2}}=2 \mathrm{m}, b=1 \mathrm{m}$であるものとして，圧力中心位置$\zeta $を求めなさい．

解答　本文中の式(3.1)を用いて求める．

\begin{eqnarray*}
\zeta &=& \frac{1}{HA}\int^{z_2}_{z_1}{z^2~b~dz} \\
&=& \frac{1}{\left(1.5 \mathrm{m}\right)\mathrm{\cdot }\left(\mathrm{1}{~\mathrm{m}}^{\mathrm{2}}\right)}\cdot \frac{1}{3}\left[{\left(2~\mathrm{m}\right)}^3-{\left(1~\mathrm{m}\right)}^{\mathrm{3}}\right]\mathrm{\cdot }\left(\mathrm{1}~\mathrm{m}\right) \\
&=& \frac{\mathrm{14}}{\mathrm{9}}~\mathrm{m}~\mathrm{\simeq }~\mathrm{1.56}~\mathrm{m}
\end{eqnarray*}
圧力中心は重心よりも 約6 cm 深い位置にある．

---

演習問題3-2　水中にある球体に働く浮力

半径 $r_s\mathrm{=5}~\mathrm{cm}$ の球体をワイヤで吊るし，その重量をばねばかりで測定したところ，空気中での重量表示は $W_A\mathrm{=20}~\mathrm{N}$ であった．球体がすべて水に沈んだ状態で同様に重量を測定した場合，ばねばかりの重量表示値 $W_B$ を求めなさい．水の密度 $\rho \mathrm{=1000}~\mathrm{kg/}{\mathrm{m}}^{\mathrm{3}}$, 重力加速度の大きさ $g\mathrm{=9.81}~\mathrm{m/}{\mathrm{s}}^{\mathrm{2}}$ であり，ワイヤの重量および体積は無視できるものとする．

解答　水中にある球体に働く浮力の分，ばねばかりの重量表示値は小さくなる．球体に働く浮力の大きさ $B$ は球体が押しのけた水の重量に等しい．球体の体積を $V_s$ とすると，$B=\rho gV_s$ である．ここで，$V_s=\frac{4}{3}\pi r^3_s$ であるため，

\begin{eqnarray*}
B&=& \rho g\cdot \frac{4}{3}\pi r^3_s\\
&=&(1000~\mathrm{kg/}{\mathrm{m}}^{\mathrm{3}})\cdot (9.81 \mathrm{m/}{\mathrm{s}}^{\mathrm{2}})\cdot \frac{4}{3}\pi \cdot {\left(0.05~\mathrm{m}\right)}^3\\
&\simeq& \mathrm{5.14 N}
\end{eqnarray*}

よって，$W_B=W_A-B=14.9 \mathrm{N}$ となる．

---

＜正員＞ 守 裕也

◎電気通信大学　大学院情報理工学研究科　准教授

◎専門：流体力学，熱流体制御

＜正員＞ 中 吉嗣

◎明治大学　理工学部　機械工学科　准教授

◎専門：流体力学，乱流計測