---

本連載を書籍化した、「基礎からの材料力学 (JSMEやさしいテキストシリーズ) 」が発行されました。機械工学への新たな一歩を踏み出す学生の方々、学びなおしの一冊として教科書をお探しの社会人の方々にふさわしい新定番の教科書です。　Kindle版　／　単行本（ソフトカバー）版　

YouTubeで「JSMEやさしいテキストシリーズ”材料力学”」の紹介動画が視聴できます！
第5回：トラス(19:58)

---

1　はじめに

機械構造物や建築構造物は，いくつかの構造要素（部材）から構成されている。今回は，複数の部材からなる構造のなかでもっとも基本的なトラスについて考える。トラスは骨組構造を構成する要素が，結合部において互いに回転自由となるように結合されている構造であり，結合要素間では荷重（軸力）のみが伝達される点に特徴がある。典型的なトラス構造について，静定問題および不静定問題の解き方を解説する。

2　静定トラス

図4.1に示すように，2本の部材からなるトラス構造について考える。各々の部材は点A，点Cにて剛体壁に回転自由となるように取り付けられており，さらに点Bにおいて2本の部材は回転自由になるよう結合されている。2つの部材はともに長さ$l = 500[{\rm mm}]$，直径$d = 5[{\rm mm}]$の丸棒であり，ヤング率は$E = 206[{\rm GPa}]$，線分ACと部材とのなす角は$\theta = 30^\circ$である。結合点Bにおいて，図の下向きに荷重$P = 2[{\rm kN}]$が作用している。結合点Bにおける変位，部材に作用する応力を求めよう。

 図4.1　静定トラスの変形

部材AB，部材CBに作用する軸力（引張を正とする）を$Q$とおく。図4.2に示すように，結合点において，2つの部材からの反力$Q$と外力$P$がつり合うことより，

\[P = 2Q \sin \theta, \quad \therefore \ Q = \frac{P}{2 \sin \theta}\]

部材の断面積を$S$とおくと，部材に生じる応力$\sigma$と伸び$\lambda$はそれぞれ，

\[\sigma = \frac{Q}{S} = \frac{P}{2S \sin \theta}, \quad \lambda = \frac{\sigma}{E} l = \frac{Pl}{2S E \sin \theta}\]

部材の変形が微小であるとすれば，トラスの角度$\theta$の変化も微小であるものとみなしてよい。この仮定をおくと，変位$\delta$（図4.3のBB’）と棒の伸び$\lambda$のあいだに

\[\lambda = \delta \sin\theta\]

の関係が成立する。よって荷重点の変位$\delta$は，

\[
\begin{split}
\delta &{}= \frac{\lambda}{\sin\theta} = \frac{Pl}{2SE \sin^2 \theta} = \frac{2 Pl}{\pi d^2 E \sin^2 \theta} \\
&{} = \frac{2 \times 2000 \times 500 \times 10^{-3}}{(3.14\ldots) \times (5.0 \times 10^{-3})^2 \times 206 \times 10^9 \times 0.5^2} \\
&{} = 4.944 \times 10^{-4} = 494 [\mu {\rm m}] \quad (\text{答})
\end{split}
\]

部材に作用する応力は以下のように求められる。

\[
\begin{split}
\sigma &{}= \frac{Q}{S} = \frac{2P}{\pi d^2 \sin \theta} = \frac{2 \times 2000}{(3.14\ldots) \times (5.0\times10^{-3})^2 \times 0.5} \\
&{} = 101.8 \times 10^6 = 102 [{\rm MPa}] \quad (\text{答})
\end{split}
\]

 

図4.2　荷重のつりあい

図4.3　変位間の関係

3　直交する2方向の荷重を受ける静定トラス

図4.4に示すような，点A，Bで剛体壁に結合され，さらに点Cにおいて互いに結合された2本の部材からなるトラス構造について考える。なお，点A，B，Cではすべて回転自由となるように結合されている。2本の部材の断面積は$S$，長さは$l$，ヤング率は$E$である。結合点Cにおいて，水平方向（図の右向き）に荷重$P_{\rm H}$を，鉛直方向（図の下向き）に荷重$P_{\rm V}$を作用させるものとする。このトラスの結合点Cにおける水平方向変位$\delta_{\rm H}$，鉛直方向変位$\delta_{\rm V}$を求めよう。部材ACに作用する荷重を$P_{\rm AC}$，部材BCに作用する荷重を$P_{\rm BC}$とする。水平方向と鉛直方向に対して力のつりあいを考えると，

\[ \frac{P_{\rm AC}}{\sqrt{2}} + \frac{P_{\rm BC}}{\sqrt{2}} = P_{\rm H}\]

\[\frac{P_{\rm AC}}{\sqrt{2}} – \frac{P_{\rm BC}}{\sqrt{2}} = P_{\rm V}\]

これらの2式を連立して解き，$P_{\rm AC}$，$P_{\rm BC}$を求めると，

\[P_{\rm AC} = \frac{1}{\sqrt{2}} (P_{\rm H} + P_{\rm V})\]

\[P_{\rm BC} = \frac{1}{\sqrt{2}} (P_{\rm H} – P_{\rm V})\]

よって部材AC，部材BCの伸びはそれぞれ，

\[\lambda_{\rm AC} = \varepsilon_{\rm AC} l = \frac{\sigma_{\rm AC} l}{E} = \frac{P_{\rm AC} l}{E S} = \frac{(P_{\rm H} + P_{\rm V}) l}{\sqrt{2} E S}\]

\[\lambda_{\rm BC} = \varepsilon_{\rm BC} l = \frac{\sigma_{\rm BC} l}{E} = \frac{P_{\rm BC} l}{E S} = \frac{(P_{\rm H} – P_{\rm V}) l}{\sqrt{2} E S}\]

部材の伸び$\lambda_{\rm AC}$，$\lambda_{\rm BC}$を図示すると図4.5のようになる。

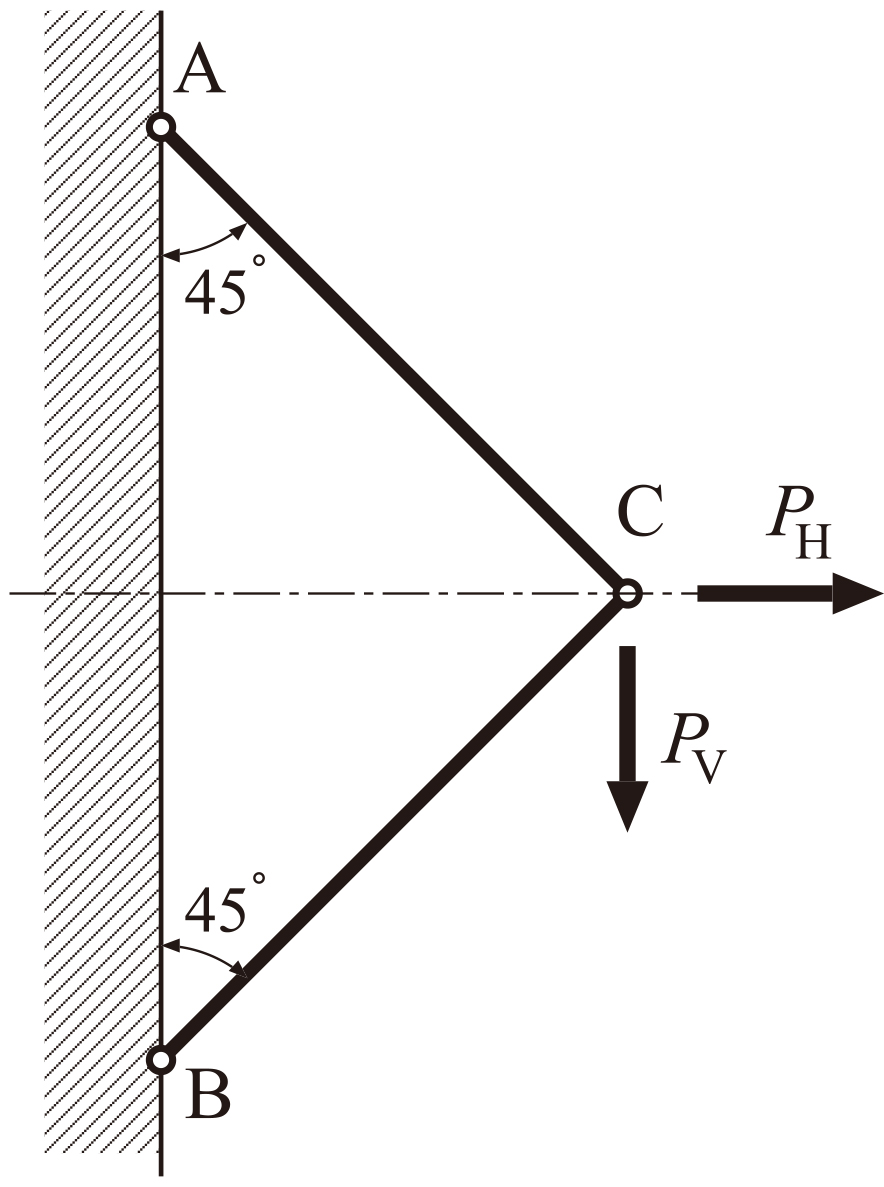
図4.4　直交する2方向に荷重を受ける静定トラス

図4.5　トラスの伸びと荷重点変位の関係

よって図4.5より水平方向変位$\delta_{\rm H}$，鉛直方向変位$\delta_{\rm V}$が以下のように求められる。

\[\delta_{\rm H} = \frac{1}{\sqrt{2}} \lambda_{\rm BC} + \frac{1}{\sqrt{2}} \lambda_{\rm AC} = \frac{P_{\rm H} l}{ES} \quad (\text{答})\]

\[\delta_{\rm V} = \frac{1}{\sqrt{2}} \lambda_{\rm AC} – \frac{1}{\sqrt{2}} \lambda_{\rm BC} = \frac{P_{\rm V} l}{ES} \quad (\text{答})\]

4　不静定トラス

図4.6に示すような3本の丸棒部材からなるトラス構造がある。部材AF，BF，CFはそれぞれ点A，B，Cで回転自由となるように固定されており，3本の部材が回転自由に結合された点Fにおいて図の下向きに荷重$P$が作用している。3本の部材の断面積は$S$，長さは$l$，ヤング率は$E$である。また，部材AFと部材BF，部材CFと部材BFのなす角度は$\theta$である。荷重点Fにおける変位を求めよう。

図4.6　不静定トラス

まず，部材AF，CFに作用する軸力を$Q_1$，部材BFに作用する軸力を$Q_2$とおく（ともに引張が正）。$Q_1$，$Q_2$と外力$P$との間には以下の関係式が成立する。

\[P = 2 Q_1 \cos\theta + Q_2\]

(1)

部材AF，CFの伸びを$\lambda_1$，部材BFの伸びを$\lambda_2$とし，それらを$Q_1$，$Q_2$で表すと，

\[\lambda_1 = \varepsilon_1 l = \frac{\sigma_1 l}{E} = \frac{Q_1 l}{ES}\]

(2)

\[\lambda_2 = \varepsilon_2 l = \frac{\sigma_2 l}{E} = \frac{Q_2 l}{ES}\]

(3)

図の上下方向の変形について考えると，伸び$\lambda_1$と$\lambda_2$には

\[\lambda_1 = \lambda_2 \cos \theta\]

(4)

の関係が成立するから，式(2)，(3)を式(4)に代入して，

\[Q_1 = Q_2 \cos\theta\]

(5)

式(1)，式(5)を連立させて軸力$Q_1$，$Q_2$を求めると，

\[Q_1 = \frac{P \cos \theta}{1 + 2\cos^2\theta}\]

\[Q_2 = \frac{P}{1 + 2\cos^2\theta}\]

最終的に荷重方向の変位$\delta$は以下のようになる。

\[\delta = \lambda_2 = \frac{Q_2 l}{ES} = \frac{Pl}{ES(1 + 2\cos^2\theta)} \quad (\text{答})\]

 

図4.7　部材の変位$\lambda_1$，$\lambda_2$の関係

 

演習問題 4.1：正方形状の静定トラス

図4.8に示すような対角線BDに部材が入った正方形状のトラスについて，点A，Cに図に示す向きの荷重$P$を作用させた。部材BDに作用する荷重$Q_{\rm BD}$と部材BDの伸び$\lambda_{\rm BD}$を求めよ。なお，すべての部材のヤング率は$E$，断面積は$S$である。

図4.8　正方形状の静定トラス

 

（答：$\boldsymbol{Q_{\rm BD} = P,\ \lambda_{\rm BD} = \dfrac{\sqrt{2} Pl}{ES}}$）

---

＜フェロー＞

荒井 政大

◎名古屋大学 工学研究科航空宇宙工学専攻 教授

◎専門：材料力学，固体力学，複合材料。有限要素法や境界要素法による数値シミュレーションなど。

---